算数の円の面積を計算する方法

学習する学年：小学生

１．円の面積を求める公式

小学校に通っていた頃に円の面積を求める公式を先生から教わりましたよね。

しかしながら、社会人になって技術系の仕事をしている人以外では、円の面積を求める式を使う機会がほとんどないので覚えてすらいないのではないでしょうか。

円の面積は、小学生の高学年の時に次の式を使って計算しなさいと教わりました。

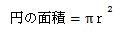
円の面積の公式とは、円の計算の授業で呪文のように唱えて覚えたお馴染みのパイ・アールの2乗です。

円の面積の公式は思い出せましたか。思い出せない方は、円の面積はパイ・アールの2乗と覚えてください。

なお、パイとは円周率のことで3.14、アールとは円の半径のことなので、記号を使って表わすと、

• 円の面積＝3.14×r×r

記号を使わずに言葉で表すと、

• 円の面積＝円周率×半径×半径

という式になります。

この式を使えば円の面積を求めることは簡単にできますが、円の面積を求める式がなぜπr²（円周率×半径×半径）なのかについて以下で説明していきます。

２．円の面積の公式をわかりやすく説明

円の面積は上の説明を読んでパイ・アールの2乗ということがわかりました。

では、どうして、円の面積はパイ・アールの2乗という式になるのか考えていきましょう。

言葉だけで説明してもイメージがわかないと思いますので図を使って説明します。まずは下の図を見てください。

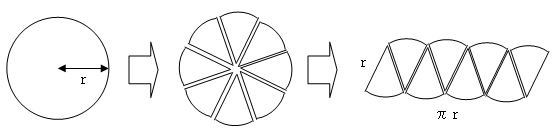
この図は、円を8等分に分けた後に、長方形になるように工夫してつなぎ合わせた図です。

この状態ですと、まだ長方形にはなっていませんが、円を8等分ではなく100等分とかもっと細かく分けてつなぎ合わせると長方形になります。

ここで、長方形の面積を求める式を思い出してください。

長方形の面積は、「たて×よこ」で求められますよね。

円の面積も、円を細かくして長方形になるようにつなぎ合わせていけば、「たて×よこ」で求められるということです。

上の図の一番右の図を見てください。この長方形のたてとよこは、次のように表すことができます。

• たて＝半径＝r
• よこ＝半円周＝円周率×半径＝πr

よこを別の考え方で表すと、円周＝2πr（読み方：ニイ・パイ・アール）ですので、よこ＝半円周＝円周÷2でも求められます。

したがって、円の面積の式は、たて×よこ＝r×πrなので、

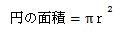
という式になり、学校で教わった式になります。

円の面積を求める公式の成り立ちが理解できたでしょうか。

３．円の面積の計算方法

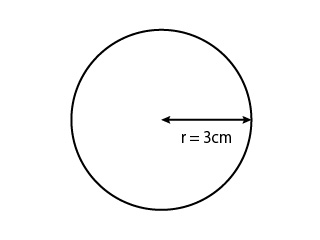
円の面積を求める公式がわかってもらえたところで、次は実際に上の円の面積を数値を使って計算してみましょう。

図形で与えられている数値を式に代入するだけで答えはでますので難しく考えなくても大丈夫です。

円の面積の公式は次の式ですよね。

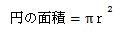
上の式を計算するのに必要な数値は、半径の数値なので、上の図形から値を読み取ってください。

読み取った値は次のようになります。

• 半径：3cm

半径の値が読み取れましたら、数値を式πr²に代入して計算しましょう。

πの値はわかりますか。πは3.14です。

• 円の面積＝π×3²＝3.14×3×3

式を計算すると答えは28.26cm²になります。

４．おうぎ形の面積の計算方法

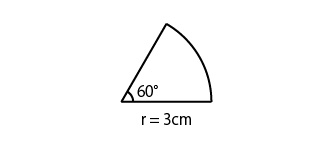
円の面積の求め方がわかってもらえたところで、次は円の形を中心点から切ったおうぎ形の面積を数値を使って計算してみましょう。

おうぎ形の面積を求める式は、円の面積の式を使った応用ですので難しくありません。

おうぎ形の面積を計算する式の作り方は次の通りに行ってください。

1. 半径rの円の面積を求めます。
2. 360°の内のおうぎ形の角度は何度になっているのかを使って円の面積を掛け合わせて計算します。

つまり、おうぎ形の面積を求める式は次のようになります。

それでは、上の図形のおうぎ形の面積を求めてみましょう。

図形で与えられている数値を式に代入するだけで答えはでますので難しく考えなくても大丈夫です。

おうぎ形の面積の式に代入する値は、円の面積を求める半径とおうぎ形の中心角が必要になるので次の2つです。

• 円の半径＝3cm
• おうぎ形の角度＝60°

それでは、おうぎ形の面積を求める式に値を代入してみましょう。

• おうぎ形の面積＝円の面積×おうぎ形の角度/360°
• ＝π×r²×おうぎ形の角度/360°
• ＝3.14×3²×60°/360°
• ＝3.14×3×3/6
• ＝4.71

式を計算すると答えは4.71cm²になります。

なお、円の面積でもおうぎ形の面積でも面積の単位は、cm²、m²のように2がつきますので間違えないようにしてください。