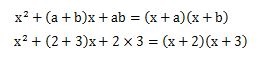因数分解
学習する学年:中学生
1.因数分解の説明
因数分解という言葉を聞いて、中学生の時に、結構苦労した思い出がよみがえってくる方もいるのではないでしょうか?
因数分解は、いったい何をやっているのか言葉の意味がわからない方は大勢いますよね。因数分解を因数と分解という別々の言葉に置き換えて考えてみましょう。
- 因数とは、1つの式や数字が2つ以上の式や数字の積で表される時の数字や式のことをいいます。
- 分解とは、1つにまとまっているものをいくつかのものに分けることです。
ですので、この、因数分解という言葉は簡単にまとめてしまえば、式を展開することの逆バージョンであるといえます。
例えば、15という数は、
- 3×5
で表されます。
この3や5の数が因数となります。
例えば、
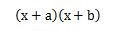
という式は、(x+a)と(x+b)が因数となります。整式の積を構成しているもののことが因数です。
どういうものが因数か理解できましたか?
要するに、因数分解とは、1つの整式を複数の整式の積で表すことです。複数の整式の積を展開すると1つの整式で表すことができ、展開した整式を因数分解すると複数の整式の積で表すことができます。
展開は機械的にできるので易しいと思いますが、因数分解はテクニックや経験が必要になってきますので解くのは厄介です。
因数分解する方法は、主にたすき掛けを使う方法と公式を使う方法の2種類があります。
どちらを使って解けばいいのかは各自で使いやすい方で構いません。問題の複雑さによって使いやすさが変わってきますので、いろいろ試してみてください。
下で、たすき掛けを使う方法と公式を使う方法を説明しますので、どちらかの方法で因数分解をできるようにしてください。
2.たすき掛けを使って因数分解する方法
たすき掛けを使う方法は計算が一見複雑そうに見えますが、コツを覚えれば簡単に行えますので覚えておいて損はありません。
むしろ、公式よりもたすき掛けの方が使う頻度は高いと思いますし、使い道はたくさんありますので解き方を1通り覚えておいてください。
それでは、次の方程式を因数分解して、その後に解を求めてみましょう。
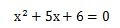
手順1.
上記の式のそれぞれの項から、x2の係数の1、xの係数の5、定数項の6を抜き取ります。
※係数とは未知数の前の符号と数字のことです。
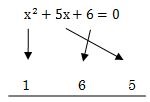
手順2.
次は、x2の係数の1の計算を始めます。
計算方法は、何かと何かを掛け合わせたら+1になる何かの数を書き込みます。
この場合は、1×1=1なので1と1を書き込んでみます。
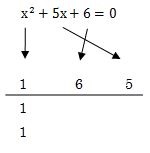
手順3.
その次は、定数項の6の計算を始めます。
計算方法は、何かと何かを掛け合わせたら+6になる何かの数を書き込みます。
この場合は、2×3=6なので2と3を書き込んでみます。
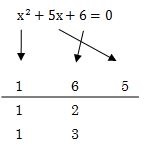
手順4.
最後は、書き込んだ数をななめに掛け合わせた数を書き込みます。
- 1×2=2
- 1×3=3
ななめに掛け合わせたら2と3になりましたよね。その数を足し合わせてみてxの係数の+5と同じ数になるか確かめます。
したがって、2+3=5になりました。
xの係数の+5と同じ数になったのでこれで計算は終了です。
もし、xの係数と同じにならない場合は、x2の係数と定数項のそれぞれの掛け算を変えていろいろ試してください。
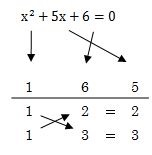
手順5.
手順4でxの係数の5と計算した数が一致したこの状態(1×1=1、2×3=6、2+3=5)で、次のように上下2段の数を横方向に抜き取りxを付け加えます。
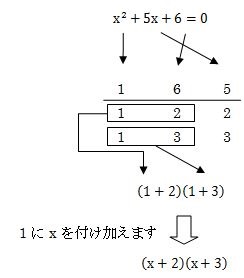
よって、たすき掛けで因数分解した答えは次のようになります。
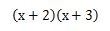
(x+2)(x+3)になるまでが因数分解の計算ですが、解といわれるxの値を知りたいと思いませんか。
解とは、方程式=0が成り立つxの値のことです。
それでは、(x+2)(x+3)=0から解を求めてみましょう。
xの値を求めると、x+2=0、x+3=0となる値を求めればいいので、答えはx=-2と-3になります。
x=-2と-3が合っているか確認する為に、初めの式のx2+5x+6=0に、ここで求めたxの値を代入して確かめてみましょう。
- x=-2の時:4-10+6=0
- x=-3の時:9-15+6=0
どちらも0となりましたので解のx=-2と-3は正しいことがわかりました。
3.公式を使って因数分解する方法
公式を使って因数分解する方法は、式を公式に当てはめて使います。
公式を使った方が簡単にできそうに思えますが、公式を覚えるのに時間が掛かかりますので、たすき掛けと併用した方がいいです。
下によく使う公式を載せておきますので使ってください。
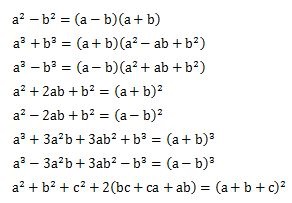
こういう公式もあります。
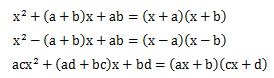
今回の上で解いたたすき掛けを使った問題は、下の公式を使えば解けます。時間がある方は公式を使って解いてみてください。