式の展開
学習する学年:中学生
1.式の展開の説明
中学生になると数学の授業で式の展開の勉強が始まります。
みなさんは式の展開はできますか?
展開とは、複数の整式(3xなどの単項式と2x+yなどの多項式を合わせたもの)の積を1つの整式で表すことです。
つまり、(x+a)(x+b)の複数の整式をx2+(a+b)x+abにすることです。1つの整式になっていますよね。
ちなみに、(x+a)(x+b)の式のことを、1つの整式を複数の整式の積で表しているので因数分解といいます。
まずは、下の用語の意味の違いを覚えてください。
- 式の展開:x2+(a+b)x+ab
- 因数分解:(x+a)(x+b)
中学校で勉強する数学が苦手な方のほとんどは式の展開が理解できなくて、数学の授業についていけなくなったからではないでしょうか。
そして、式の展開と平行して因数分解という厄介なものが現れて、さらに数学が苦手になっていくパターンが考えられます。
式の展開は、因数分解みたいに難しくはありませんので、基本的なルールにしたがって解いていけば時間はかかりますが答えを導くことはできます。
ですので、式を展開するためのルールを覚えてください。
基本的には、それぞれの項を順番に掛け合わせてから足していく作業になります。地道な作業ですが基本通り計算すれば答えは導きだせます。
2.式を展開する1
それでは、実際に下の式を展開してみましょう。
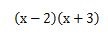
この式の解き方は、それぞれの色の矢印の始点の項と終点の項を掛け合わせたものを足していきます。
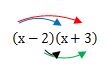
この式を矢印の色に沿って解いていくと、このようになります。

したがって、展開した答えは次のようになります。
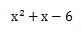
答えは、x2+x-6です。
3.式を展開する2
それでは、次の式を展開してみましょう。
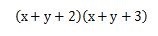
式の展開は、項の数が増えても基本的に「式を展開する1」で説明したように、項を1つずつ順番に掛け合わせていき、掛け合わせた項を足していく作業です。
この式も同じ要領で解いていけます。
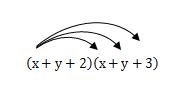
式を展開した答えは、次のようになります。
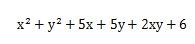
途中式を考えながら自分で解いてみましょう。
4.式を展開する3
最後に、次の式を展開してみましょう。
2乗の式ですがどうやって展開を進めていきましょうか?
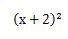
この式は、2乗をなくすとこのようになります。
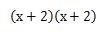
後は、同じ要領で解いていってください。
展開した答えは、次のようになります。
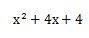
答えは、x2+4x+4です。
頑張って式の展開のルールを勉強してもらえれば数学が得意な科目になっていきます。
