数学の実数の説明

学習する学年：中学生

１．実数を構成する数

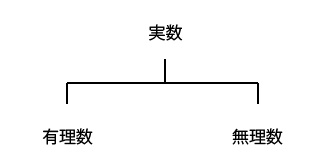
数学の教科書には実数、整数、小数という言葉はよく出てきます。

実数とは、有理数と無理数を合わせた数のことです。

有理数と無理数をわかるように簡単に説明します。

有理数とは、次のように整数と有限小数と循環小数の3つの数のことです。

整数

整数とは、自然数、ゼロ、負の整数のことです。

例としては、3、2、1、0、－1、－2、－3の数のことです。

有限小数

有限小数とは、有限の小数で分数にできる小数のことです。

例としては、0.5＝1/2、0.25＝1/4、0.2＝1/5、0.125＝1/8の数のことです。

循環小数

循環小数とは、小数点以下の数が繰り返し現れ分数にできる小数のことです。

循環する無限小数も含まれます。例としては、0.142857…＝1/7、0.703…＝19/27、0.3333…＝1/3の数のことです。

つまり、有理数とは、小数点がつかない整数と小数点がついても分数に変換できる数のことです。

では、無理数はどのような数かというと次のような数のことです。

無理数

無理数とは循環しない無限小数のことです。

例としては、√2＝1.4142…、√3＝1.732…、π＝3.1415…の数のことです。

つまり、無理数とは、小数点がついて分数に変換することができない数のことです。

したがって、有理数と無理数とは、具体的には、整数、小数、分数、平方根、π（パイ） などの数のことです。

これらの有理数と無理数で幾何学的な数直線は埋め尽くされていっぱいになりますので、実数は数直線上に必ず存在していることがいえます。
※数直線は、実数をすべて点で直線上に表すことができます。

この実数の数直線上に表すことができない数は虚数 という概念を使って、もう1つの虚数の直線を使い表します。
※横軸は実軸、縦軸は虚軸を作り2次元の数にします。