球の計算
学習する学年:小学生
1.球の説明

球体とは、球の中心から等距離に描かれる丸いボールの形をしている物体のことです。
身近にある球の形では、野球のボール、テニスボール、ビー玉、スーパーボールなどの形をイメージしてもらうとわかりやすいと思います。
ここで、みなさんに気をつけてもらいたいことは、間違えやすい図形の形として円と球があります。
- 円は縦と横の軸の2次元で表し平面図形で描くもの
- 球は縦と横と高さの3次元で表し立体図形で描くもの
つまり、円は平面図形なので面積を求める問題がよく出題され、球はその立体の空間内のすべてを表している立体図形なので、球の表面積と体積を求める問題がよく出題されます。
円と球は平面図形か立体図形かの違いがありますので形を間違えないようにしてください。
球は3次元で表す丸い形の立体図形であることを覚えておいてください。
2.球の表面積を求める方法
球の表面積の求め方を考えてみましょう。
球の表面積は、円の面積の4倍の大きさになります。
表面積とは立体図形の表面だけの面積のことです。
下の球の図を見てください。
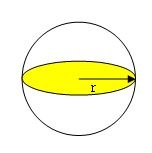
この球体を切りきざんでいくと次のような形になります。
(おおざっぱな図ですので、さらに細かく切りきざんでください。)
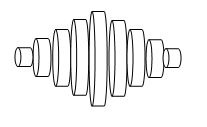
切り刻んだ小さな円柱の側面の表面積をそれぞれたしていくと、円の面積の4倍になります。
(積分を使って計算していくと4倍になることがわかります。時間がある方は計算してみてください。)
よって、半径をrとすると、球の表面積の式は、

になります。
3.球の体積を求める方法
球の体積は、小さな三角錐に近い形をしたものを足し合わせていくと求めることができます。
下の図を見てください。
この図は、球を三角錐の集まりにした図です。rとは半径のことです。
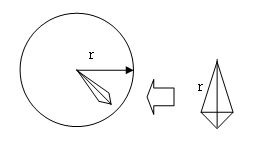
三角錐に近い形をした体積を求めるには、三角錐の体積の式を使ってほぼ計算することができます。

それでは、球の体積を求めてみましょう。
球の体積は、三角錐を足し合わせたものなので、

になります。
この式のすべて足し合わせた三角錐の底面積を別の言葉でいいかえれば、次のようになります。

よって、式を整理すると、球の体積の式は、
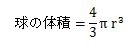
になります。
