錐(すい)の図形の形と体積の計算
学習する学年:小学生
1.錐(すい)の説明
錐(すい)とは錐体(すいたい)のことです。
錐体は、頂点を1点とした図形で、底面の形は円、三角形、四角形となるような下の図のような立体図形のことをいいます。
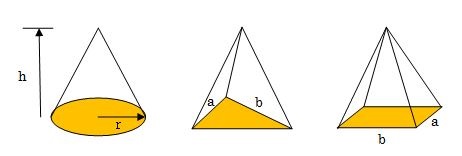
上記のそれぞれの立体図形は、円錐(えんすい)、三角錐(さんかくすい)、四角錐(しかくすい)といい、それぞれの特徴は次のようになります。
- 円錐:頂点の数は1つ、辺の数は0、面の数は2つの図形
- 三角錐:頂点の数は4つ、辺の数は6つ、面の数は4つの図形
- 四角錐:頂点の数は5つ、辺の数は8つ、面の数は5つの図形
もっと簡単に錐体を説明すれば、立体図形の頂点がとんがっているものは錐体といえます。
錐(すい)体の体積を計算する方法は、次の式のように柱の体積を求める式を3で割ってもらうと求めることができます。

それでは、円錐、三角錐、四角錐の体積を実際に求めてみましょう。
2.円錐の体積の計算
下の図が円錐の立体図形です。
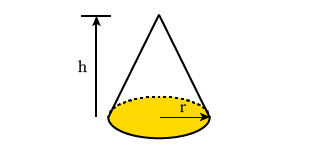
円錐の底面は円になっていますので、円の面積を計算する式と高さを使えば体積を求めることができます。

円錐の底面積と高さを掛け合わせましたら、後はその値を3で割ってください。
したがって、円錐の体積を求める式はこのようになります。
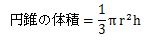
それでは、実際に円錐の体積を求める式に数字を入れて計算してみましょう。
次のように円錐の底面の半径と高さが与えられた時の体積を求めてください。
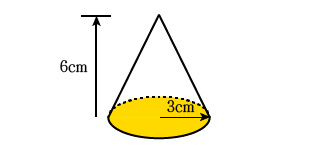
式に数値を当てはめて計算した答えは、次のようになります。
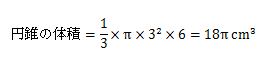
このように、円錐の体積は、底面積×高さ÷3を計算してもらうと求めることができます。
3.三角錐の体積の計算
下の図が三角錐の立体図形です。
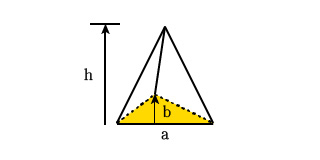
三角錐の底面は三角形になっていますので、三角形の面積を計算する式と高さを使えば体積を求めることができます。

三角錐の底面積と高さを掛け合わせましたら、後はその値を3で割ってください。
したがって、三角錐の体積を求める式はこのようになります。
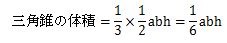
それでは、実際に三角錐の体積を求める式に数字を入れて計算してみましょう。
次のように三角錐の底面の長さと高さが与えられた時の体積を求めてください。
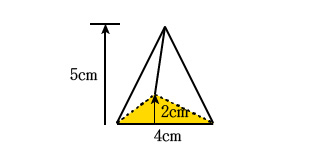
式に数値を当てはめて計算した答えは、次のようになります。
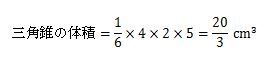
このように、三角錐の体積は、底面積×高さ÷3を計算してもらうと求めることができます。
4.四角錐の体積の計算
下の図が四角錐の立体図形です。
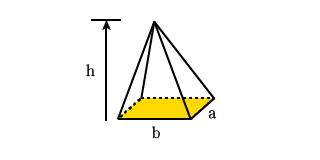
四角錐の底面は四角形になっていますので、四角形の面積を計算する式と高さを使えば体積を求めることができます。

四角錐の底面積と高さを掛け合わせましたら、後はその値を3で割ってください。
したがって、四角錐の体積を求める式はこのようになります。
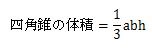
それでは、実際に四角錐の体積を求める式に数字を入れて計算してみましょう。
次のように四角錐の底面の長さと高さが与えられた時の体積を求めてください。
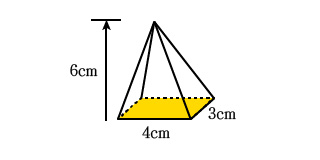
式に数値を当てはめて計算した答えは、次のようになります。
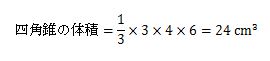
このように、四角錐の体積は、底面積×高さ÷3を計算してもらうと求めることができます。
今まで錐体の体積の計算をする時に、普通に3で割ってきましたが、なぜ3で割るのでしょうか?
それは、高校や大学で出てくる積分を使うと3で割ることがわかります。少し難しい話になりますので、興味がある方は積分を勉強してみてください。
