数学の2次関数（2次方程式）のグラフの説明

学習する学年：中学生

１．2次関数（2次方程式）y=x²のグラフの説明

中学校で勉強する関数は、1次関数、2次関数があります。

今回は、2次関数（方程式）のグラフについて考えてみます。

2次関数とは、未知数の一番大きい次数が2になっている関数の式のことをいいます。

次数とは、ｘ²を例にすると、エックスの2乗という何乗の部分のことです。この何乗の部分が2になっている式が2次関数となります。

ちなみに、xの何乗の部分がない式（何乗の部分が1になっている意味）が1次関数です。

それでは、次の2次関数の式をグラフに描いてみましょう。

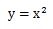
グラフとは関数（方程式）を満たす点の集合のことです。

y=ｘ²の式をグラフに描くと下のようになります。

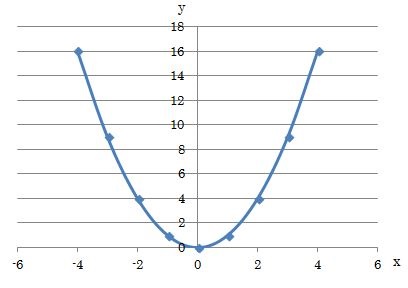
グラフを描く時はどのように行えばいいのかというと、増減表を作れば簡単にできます。

式のxに値を代入してyを求めた増減表を作ると次のようになります。

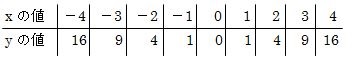
この増減表で求めたx、yの値をプロットして線を引けばグラフを描くことができます。

グラフを見ると、y軸を対象軸として曲線を描いていることがわかると思います。

この2次関数のグラフの曲線のことを放物線といい、y軸を中心として左右対称となります。

詳しくは、2次関数 でもふれていますので参考にしてください。

また、グラフが一番ふくらんで向きが反転する位置（x＝0、y＝0）を放物線の頂点といいます。

この場合は頂点がyの値が一番小さくなるので最小値となります。

このように、下に頂点を持ち上に開いた放物線のグラフのことを下に凸（したにとつ）といいます。

２．2次関数（方程式）y=-x²のグラフの説明

次は、マイナス符号がついた2次関数の式を見ていきましょう。

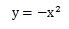
y=-ｘ²の式を増減表を作ってグラフに描くと下のようになります。

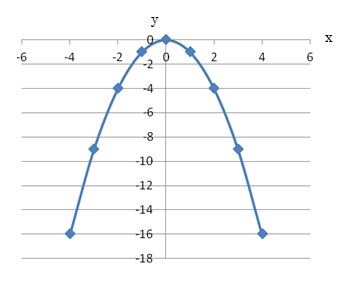
このグラフは、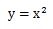の向きを上下反転していることがわかります。

このように、上に頂点を持ち下に開いた放物線のグラフのことを上に凸（うえにとつ）といいます。

この場合は頂点がyの値が一番大きくなるので最大値となります。

上の2つのグラフを比べると、式にマイナスが付いている時と付いていない時の違いがわかったと思います。

次数が2の係数がプラスの時は下に凸の放物線、マイナスの時は上に凸の放物線となります。

３．2次関数（方程式）y=x²＋1のグラフの説明

最後に、次の2次関数の式を考えて見ましょう。

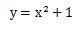
y=-ｘ²＋1の式をグラフに描くと下のようになります。

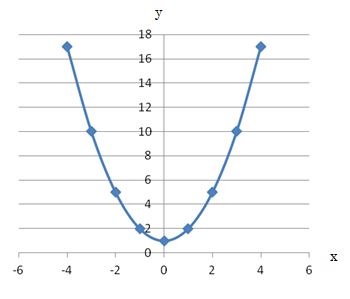
このグラフは、頂点の位置がいままでのグラフと違います。

これは1次関数（方程式）のグラフで説明したように、切片が1になっているからです。

よって、（x＝0、y＝1）が頂点になります。

1次関数はどこでも傾きは同じでしたが、2次関数では場所によりyの変化分「傾き」は変わってくるので注意してください。

2次関数のグラフは、下に凸（したにとつ）、上に凸（うえにとつ）、切片があることが理解できたでしょうか。