落下運動について
学習する学年：高校生
１．落下運動の説明
落下運動とは、物理の授業で勉強する物理数学の内容ですが、数学の知識を使うので簡単に説明したいと思います。
ものの運動や重力について勉強する時に、初心者がつまずきやすいところは落下運動です。
例えば、ビルの上から物体を落とした時に、この物体の加速度、速度、距離をどのように求めるのか考えてみましょう。
まず、計算を始める前に重要な法則があります。次のニュートンの運動の3法則をご存じでしょうか。
- 第1法則（慣性の法則）
- 第2法則（運動方程式）
- 第3法則（作用・反作用の法則）
ここでは、みなさんもよく知っている第2法則のニュートンの運動方程式を使います。
ニュートンの運動方程式の第2法則とは、力、質量、加速度の関係について表した法則のことです。
1N（ニュートン）の力は質量1kgの物体に加速度1m/s2を生じさせることを定義したものです。
ニュートンの運動の第2法則の式を表すと次のようになります。
- Ｆ＝ｍａ
※Ｆ＝力（N）、ｍ＝質量（kg）、ａ＝加速度（m/s2）
ニュートンの運動方程式Ｆ＝ｍａ（エフイコールエムエー）は、力と質量は比例するので物体の質量が大きい程物体を動かすのに大きな力が必要、力と加速度は比例するので物体に加える力を大きくすると加速度（速度）は大きくなるということを表しています。
※加速度は、1秒間当たりに速度が変化する割合のことです。
このＦ＝ｍａの式を使って加速度の求め方について説明していきます。
２．加速度の求め方
ニュートンの第2法則を使って落下する物体に作用する重力による加速度を求めてみましょう。
地球は、g=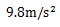
の重力加速度が生じていますので、gという重力加速度の記号を使って計算します。
加速度について計算すると次のようになります。
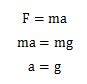
落下する物体はこの重力加速度g=9.8m/s2を受けて、加速しながら地面に向かって落ちていきます。
３．速度の求め方
次は、物体の速度を求めてみます。
物体の速度は、積分を使うと計算できます。
加速度の式は、加速度＝速度÷時間ですね。
※正確には、加速度＝（時間が経過した後の速度－初めの速度）÷経過時間
上記の式は平均の加速度を求める式です。ここでは瞬間の加速度を求める式を使いますので、次のように速度を時間で微分した式になります。
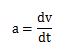
積分とは、細かくした面積を足し合わせていくことです。積分を使って、瞬間の加速度と時間の積を足し合わせていくと速度が導きだせます。
したがって、瞬間の加速度の式を、加速度の求め方で導きだしたa＝gの式に代入して、両辺を時間について積分すると速度が求められます。
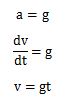
求めた速度の式を見てもらうと、物体の速度は時間に比例して速くなることがわかります。
４．距離の求め方
最後は、物体が移動する距離を求めてみます。
物体の移動距離は、積分を使うと計算できます。
まずは、速度の式を覚えていますか？
速度を求める式は、速度＝距離÷時間ですね。
※正確には、速度＝移動した距離÷掛かった時間
上記の式は平均の速度を求める式です。ここでは瞬間の速度を求める式を使いますので、次のように距離（変位）を時間で微分した式になります。
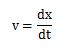
積分とは、細かくした面積を足し合わせていくことです。積分を使って、瞬間の速度と時間の積を足し合わせていくと距離（変位）が導きだせます。
したがって、瞬間の速度の式を、速度の求め方で導きだしたv＝gtの式に代入して、両辺を時間について積分すると距離が求められます。
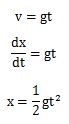
求めた距離の式を見てもらうと、物体の移動距離は時間の2乗の大きさで長くなることがわかります。
いままでの計算過程（加速度→速度→距離）は積分して求めてきましたが、計算過程を逆にして（距離→速度→加速度）にする時は微分して計算していきます。距離を微分すると速度、速度を微分すると加速度になります。
積分と微分を使って、加速度、速度、距離の求め方を練習して見てください。
少し難しいですが、加速度、速度、距離の関係 も勉強して知識を深めて見てください。
 |
 |