加速度、速度、距離の関係
学習する学年：高校生
１．加速度、速度、距離の概要
加速度、速度、距離の関係は数学ではでてきませんが、微分と積分を使いますので簡単に説明します。
物理学で使う数学のことを物理数学といいます。
物理現象を数学を使って数字や記号で表すことで工業分野は大きく発展して私たちの暮らしは豊かになりました。
加速度、速度、距離は物理数学を使って計算することが基本です。高校までは、距離はスカラーとして扱いますが、大学では変位というベクトルとして扱うようになり、加速度、速度、距離の関係は、微分、積分を使うととてもわかり易くなります。
下の図をみてください。加速度、速度、距離の関係を図にまとめました。
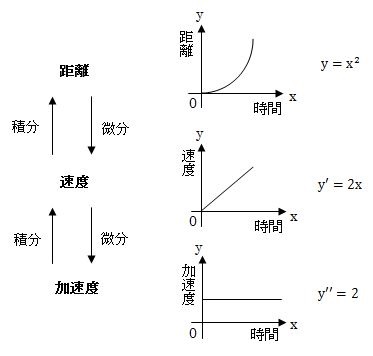
距離（変位）を微分すると速度になります。速度を微分すると加速度になります。加速度を積分すると速度になります。速度を積分すると距離（変位）になります。微分・積分を使うとこのようなルールになります。
距離、速度、加速度の計算は、微分・積分を使うことによって解決できます。
微分・積分を覚えると役に立つ場面はいろいろあります。この機会に、微分と積分の勉強を始めてみませんか。
微分と積分の意味が理解できれば物理数学も使いこなせれるようになります。
２．微分を使うと速度・加速度が計算できる
上の加速度、速度、距離の図を説明します。
速さを求める時は、高校までは、移動距離÷経過時間で計算しますよね。
この計算式では平均の速さしか求められないので、大学では、距離（変位）を時間で微分して速度を求めます。
微分をすることによって時間を限りなくゼロに近づけた時の速度が計算できるので、平均の速さではなくある瞬間の速度が求められるようになります。
加速度を求める時は、高校までは、加速度＝（ある時間経過した時の速度－初速度）÷経過時間で計算しますよね。
この計算式では平均の加速度しか求められないので、大学では、速度を時間で微分して加速度を求めます。
微分をすることによって時間を限りなくゼロに近づけた時の加速度が計算できるので、平均の加速度ではなくある瞬間の加速度が求められるようになります。
つまり、割り算して求めていた物理量は微分すれば瞬間の量が求められるということです。
例えば上の図で距離（変位）が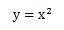
で表される時、距離の式を微分すると
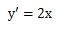になります。
さらに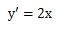を微分すると
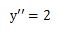になります。
よって、加速度は2とわかります。
３．積分を使うと速度・距離が計算できる
積分とは、微分の逆演算のことです。
積分とは何をしているのかというと、微小時間当たりの加速度×時間、速度×時間の面積をいくつも足し合わせるという計算をやっています。
速さを求める時は、高校までは、加速度×経過時間で計算しますよね。
この計算式では等加速度運動している時しか求められません。物体の加速度は一刻一刻変化していることが普通なので等加速度運動しているとは限らないので、大学では、加速度を時間で積分して速度を求めます。
積分をすることによって時間を限りなくゼロに近づけた時の加速度と時間の積を足し合わせた面積が計算できるので、等加速度運動ではなく加速度が変化した時にも対応できるようになります。
距離（変位）を求める時は、高校までは、速さ×経過時間で計算しますよね。
この計算式では等速運動している時しか求められません。物体の速さは一刻一刻変化していることが普通なので等速運動しているとは限らないので、大学では、速度を時間で積分して距離（変位）を求めます。
積分をすることによって時間を限りなくゼロに近づけた時の速度と時間の積を足し合わせた面積が計算できるので、等速運動ではなく速度が変化した時にも対応できるようになります。
つまり、掛け算して求めていた物理量は積分すれば積み重ねた量が求められるということです。
大学の物理では、ここで説明した微分・積分の関係は頻繁にでてきます。公式を丸暗記するのもいいと思いますが、微分、積分を使うとやさしく解けてしまうので試してみてください。
 |
 |
 |