算数の整数の普通の割り算の計算方法

学習する学年：小学生

１．整数のわりざんの計算方法

わりざんは、買い物や食事をした後の代金の支払いでよく使うことがあるわりかんをイメージしてもらうとわかりやすいと思います。

わりざんとは、ある数を他の表す数の回数だけ引き算して数を求める計算方法のことです。

例えば、50円玉を持って駄菓子屋に行って10円のうまい棒を何本買えるのか計算してみると、50÷10=5となり5本買うことができます。又は、50-10-10-10-10-10=0となり10が5回出てきたので5本買うことができます。

例えば、100円の商品の代金の支払いを2人で均等に分けてみると、1人当たり50円の支払いになりますよね。

上で述べた文章を計算式で表してみると、100÷2=50、又は、2が50回で100になります。

この計算式を、さらに計算しやすくするために下のように筆算（紙に数字を書いて計算すること）に置き換えて考えてみましょう。

まず、わりざんをする時は、間違えやすいので次のルールを覚えてください。どんなわりざんでも、「わられる数÷わる数＝」で構成されています。100÷2=をわられる数とわる数に分解してみると、

• わられる数：100
• わる数：2

に分けることができます。

そして、筆算で計算する時は、左側にわる数、その右側にわる記号、その右側にわられる数を書き込んで計算するというルールがあります。

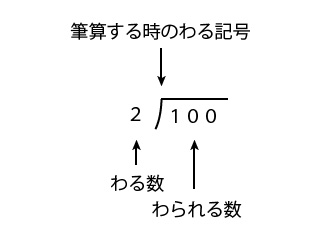
筆算でわりざんする時のルールがわかりましたら、式を筆算に置き換えた場合の計算方法の説明をします。

まず、100の数の3ケタ目（百の位）は1ですので、1÷2をしてみます。

しかし、1÷2を計算すると小数になりますので計算できません。（整数になるように計算していきます）

ですので、100の数の2ケタ目（十の位）を使って計算しなければいけません。百の位と十の位を使うと10になり、この数だと、10÷2は計算できそうです。

位についてわからない方はこちら 数のかぞえ方 を見てください。

では、答えを導いていきましょう。下の式が成り立つように四角の中に当てはまる数を探します。

四角の右側の記号（≦）の意味は、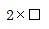が10より小さい値、又は10と同じになる値という意味です。四角の中に、5を入れるとちょうど10になりるので、筆算のわりざんのところに、100の数の2ケタ目（十の位）の上側に5を、100の数の3ケタ目（百の位）と2ケタ目（十の位）の下側に10を書き込みます。

次は、100の数の3ケタ目（百の位）と2ケタ目（十の位）を連結した10と、先ほど計算した2×5=10を引きます。10-10=0になります。0ということは余りがないことを意味しています。

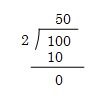
よって、次に割る数がないので100の数の1ケタ目（一の位）の上側に0を書き込んで計算は終わりです。

答えは50になります。

わりざんが非常に苦手で、わりざんを計算するイメージをつかみたい方は、こちら 四則演算が苦手な人へ２ を見てください。

２．余り（あまり）があるわりざんの計算方法

次は、答えに余りが出る時のわりざんの計算をしましょう。

上記のわりざんは余りは出てきませんでしたが、わりざんには余りが出てくることがよくあります。

次のわりざんの式を計算をしてみてください。

• 7÷3＝

暗算をしてみるとなんだかぴったり答えがでないような感じがしますね。わりざんは、答えが小数になったり余りがでたりするものなので仕方ありません。

それでは、7÷3を計算してみましょう。この式は、次のように筆算に置き換えるとわかりやすくなります。

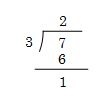
まず、次の式の四角の中を満たす一番大きい数を求めます。

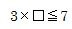
3×2=6が当てはまりそうです。

よって、四角の中は2になります。筆算のわりざんのところに2と6を書き込んでみましょう。

最後は、7-6を計算します。この計算をすると1が求まりました。この1はあまりと呼ばれていて、整数で表現したい時はこれ以上計算することができません。

答えは、2あまり1となります。

わりざんを計算するには、かけざんの九九の知識が必要になるんじゃないのかと感じた方はみえますか。

わりざんを計算するには九九の知識とかけざんの仕組みがわかっていることが重要です。

例えば、2×9=18は、18÷2=9と18÷9=2に置き換えることができるようになるので割り算の答えの予測ができるようになります。わりざんが苦手という方は九九を完璧に覚えてしまえば桁数が少ない割り算なら簡単に計算できるようになりますよ。

ここまでの説明を一通り読んでみて、割り算の計算方法はわかっていただけたでしょうか。