2進法
学習する学年:高校生
1.2進法の説明
私たちは、普段の生活では10進法という、0、1、2、3、4、5、6、7、8、9までの10個の数字をいろいろ組み合わせる方法を使って数を数えています。
しかし、数を数える方法は10進法以外にもあり、一般的には、2進法、8進法、16進法などが使われています。
2進法とは、0と1の2つの数字を使って数を表そうという方法のことです。
10進法を使って数を数えている私たちからすれば、2つの数字を使って数を表すなんてなんだかイメージができませんよね。
下の、10進法と2進法の対応表を見てください。
10進法は0~9までの10つの数字を使って数を表現しますが、2進法は0と1の2つの数字を使って数を表現します。
| 10進法 | 2進法 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
2進法は0と1しか使われていないことがわかりましたが、1の次の数はいくつになると思いますか?
10進数の時の数え方を思い出してもらうとわかります。1桁で表していた数は、桁が1つ増えて2桁で表すようになりますよね。10進法では、9の次は位が繰り上がって10です。
2進数も同じように、桁が1つ増えて2桁になります。2進法では、1の次は位が繰り上がって10となります。
10進数でも2進数でも10になりますが、10と言っても10進数の10なのか2進数の10なのかによって値が違ってきますので注意してください。
10進数の10は10進数で10ですが、2進数の10は10進数に変換すると2になります。
- 10(2進数)=2(10進数)
このように、それぞれの進数で値が変わってきますので気を付けてください。
ちなみに、2進数の読み方は、0(ゼロ)、1(イチ)、10(イチゼロ)、11(イチイチ)、100(イチゼロゼロ)、101(イチゼロイチ)と読んでいきます。
それでは、10進数と2進数の変換方法を見ていきましょう。
2.10進数から2進数への変換方法
10進数で24という数がある時、この数を10進数から2進数に変換してみましょう。
10進数から2進数に変換する手順は、次のように行ってください。
- 10進数を2で割っていきます。
- 2で割った時の余りを記入します
- 商と余りをつなぎ合わせます
10進数で24という数を2進数に変換するには、まずは、すだれ算(さかさわり算)を使って2でどんどん割っていきます。
なお、2で割った時は余りも記入してください。
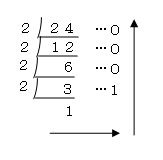
2で割れなくなるまで割ったら、次は2で割っていった商と余りの数を矢印の方向に数字を連結します。
連結方法は、上の計算結果の矢印を参照してください。
連結すると、11000になります。
よって、10進数の24(ニジュウヨン)は、2進数で11000(イチイチゼロゼロゼロ)が答えです。
3.2進数から10進数への変換方法
次は、上記の2進数で11000(イチイチゼロゼロゼロ)という数を、2進数から10進数に変換してみましょう。
変換するには、それぞれの桁に対応した重みが必要となるため指数を使います。
指数がわからない方は、こちら指数について をみてください。
2進数を下の桁から数えて、次のように重みを付けていきます。
- 桁の重みの付け方
- 1桁目は、20=1
- 2桁目は、21=2
- 3桁目は、22=4
- 4桁目は、23=8
- 5桁目は、24=16
2進数で11000という数のそれぞれの桁に対応した重み(指数)は、下のようになります。
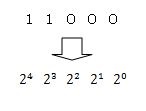
そして、2進数の11000は、下から数えて5桁目の1を24と、4桁目の1を23、と掛け合わせてそれぞれ足していきます。
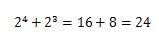
計算結果は24になります。
よって、2進数の11000は、10進数で24が答えです。
