分数のわりざんの計算手順と計算方法
学習する学年:小学生
1.分数のわりざんの説明
分数のわりざんは、分数のたしざんやひきざんを計算する時のように分母の数を揃える為に通分する必要がありませんので、とても簡単に計算して答えを出すことができます。
分数の計算という言葉を聞くと難しい印象を持つかと思いますが、分数のわりざんは特に難しく考えることはありません。分数のたしざん・ひきざんの解き方がわからないという人は分数のわりざん・かけざんから勉強を始めるのがおすすめです。
そうは言っても、分数のわりざんを行う時に必ず覚えておかなければいけないことがあります。それは、分母、分子、わる数、わられる数という言葉の意味です。
分数は分母と分子で構成されていますが、どちらが分母でどちらが分子か覚えていますか?
分数の構成は、分数の下側の数が分母で、上側の数が分子になります。
また、分数のわりざんは、わる数とわられる数を意識して計算しなければいけません。
わる数とは÷の記号の後ろ側の数のこと、わられる数とは÷の記号の前側の数のことを表しています。
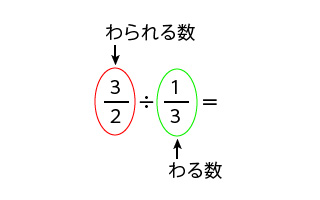
分母、分子、わる数、わられる数がわかりましたら、次は、分数のわりざんを理解するために計算するコツを覚えていきましょう。
2.分数のわりざんの計算手順
それでは、分数のわりざんの計算手順を見ていきましょう。
分数のわりざんの計算手順は、次の3ステップの内容に従って行います。
- わる数の分母の数と分子の数を入れかえます。
- わられる数と分母・分子を入れかえた数を掛け合わせます。
- 掛け合わせた答えは約分できそうなら分母と分子を約分して小さな数にします。
普通のわりざんと分数のわりざんは何が違うのかというと、分数のわりざんには約分という作業工程が発生することです。また、分数のわりざんは、分数のたしざん・分数のひきざんと何が違うのかというと分母を通分する必要がないことです。
したがって、約分の意味と計算方法がわからないと分数のわりざんの正しい答えがでません。
分数のわりざんをマスターするには、計算結果の数を小さくする為の約分という計算方法を覚えることです。
分数のわりざんが嫌いにならないようにする為に約分をしっかり覚えてから計算を始めてください。
3.2つの分数のわりざんの計算方法
上で説明した計算手順を読んで準備が整いましたら、次の分数の式を計算手順に従って計算してみましょう。
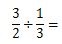
最初は、わる数(1/3)の分母の数と分子の数を入れかえます。逆数にすると3/1になります。
※分母と分子をひっくり返した分数のことを逆数といいます。
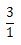
次は、わられる数(3/2)と、わる数を逆数にした(3/1)を掛け合わせます。
ここからは、分数のかけざんの計算方法と同じことをしていきます。分母どうしの数と、分子どうしの数を掛け合わせます。分母は2×1、分子は3×3を計算します。
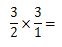
どんどん計算していきましょう。
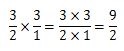
分子は3×3=9、分母は2×1=2なので、計算結果は9/2です。最後は、計算結果が約分できそうなら約分してください。
この場合は、約分ができないですね。
したがって、答えは、
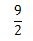
になりますが、仮分数なので帯分数にしてください。
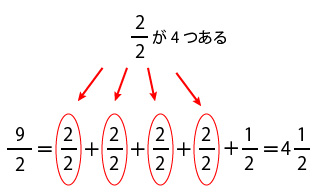
9/2は2/2を4つ含んでいるので、帯分数にした答えは4と1/2です。
4.3つの分数のわりざんの計算方法
次の分数の式を計算してみましょう。
この式には分数が3つありますが、上で解いた2つの分数のわりざんと同じ計算手順で計算できます。
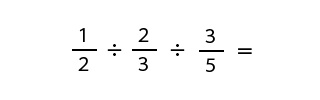
最初は、わる数の分母の数と分子の数を入れかえますので、わる数とわられる数に分けましょう。
わる数はわられる数の後ろ側なので、わる数は2/3と3/5、わられる数は1/2というように分けれます。
したがって、わる数(2/3、3/5)の分母の数と分子の数を入れかえます。逆数にすると、3/2、5/3になります。
次は、わられる数(1/2)と、わる数を逆数にした(3/2、5/3)を掛け合わせます。
ここからは、分数のかけざんの計算方法と同じことをしていきます。分母どうしの数と、分子どうしの数を掛け合わせます。分母は2×2×3、分子は1×3×5を計算します。
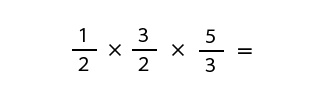
どんどん計算していきましょう。
また、約分できそうなら約分してください。かけざんの場合は計算途中でも約分しても構わないので、数が大きくなる前に約分すると計算がしやすくなります。この場合は3で割って約分ができました。
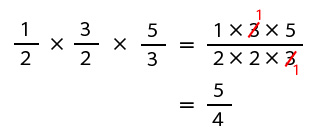
したがって、計算結果は5/4になりますが、仮分数なので帯分数にしてください。
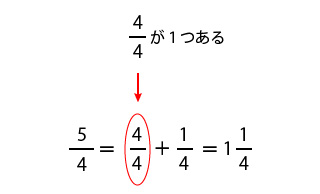
5/4は4/4を1つ含んでいるので、帯分数にした答えは1と1/4です。
5.帯分数のわりざんの計算方法
上記の分数のわりざんの計算方法がわかりましたら、次は帯分数どうしのわりざんの計算をしてみましょう。
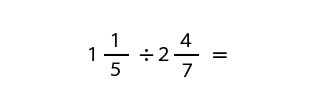
帯分数とは分数の前に数が付いている分数のことです。帯分数のわりざんの計算方法は、まずは帯分数を仮分数に変換してから、上で説明した分数のわりざんの計算手順に従って計算してもらえれば簡単に答えを導くことができます。
最初は、帯分数を仮分数に変換しましょう。帯分数を仮分数にするには帯分数の分数の前の数をなくさないといけません。
帯分数の分数の前の数は分母と分子が同じ数の分数がいくつあるかを表しています。この場合は、5/5と7/7のことです。
1/5の前の1とは5/5を1つ含んでいるということです。4/7の前の2とは7/7を2つ含んでいるということです。
したがって、次のように数の個数分の分数を足し合わせてもらえれば帯分数は仮分数へ変換できます。
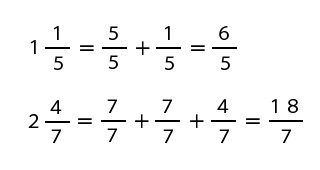
帯分数の式を仮分数の式に変えると次のようになります。
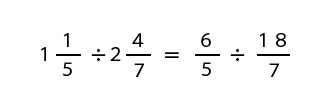
次は、わる数(18/7)の分母の数と分子の数を入れかえます。逆数にすると7/18になります。
その次は、わられる数(6/5)と、わる数を逆数にした(7/18)を掛け合わせます。
ここからは、分数のかけざんの計算方法と同じことをしていきます。分母どうしの数と、分子どうしの数を掛け合わせます。分母は5×18、分子は6×7を計算します。
かけざんの計算はこの段階で約分しても構わないので、掛け合わせる前に約分した方が早く答えが出せます。6で約分すると、分母は5×3、分子は1×7になります。
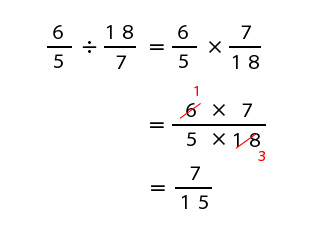
計算結果は7/15です。これ以上約分できないですし真分数なので答えは7/15です。
6.分数のわりざんを理論的に見てみましょう
分数のわりざんをする時は、わる数の分母と分子を入れかえて計算することが当たり前ですが、なぜそのようなことをしなければいけないのか理論的に見てみましょう。
まず、次の式を分数にしてください。
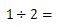
分数にできましたか?
分数にすると次のようになりますね。
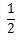
今説明したことの意味することは、わられる数(1)は分子、わる数(2)は分母になるということです。
ここまで説明したことを踏まえて、次の式を分数の形にしましょう。
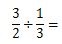
分数の形にすると下のようになりますね。
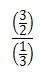
ここで、分母の数を1にするために分母と分子に3を掛け合わせます。
※分母と分子に同じ数を掛け合わせることを倍分といいます。

この形どこかで見覚えがありませんか?
わる数の分母と分子を入れかえた形になりました。
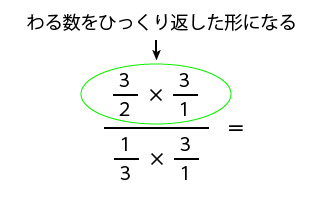
どんどん計算していきましょう。
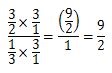
一番初めに説明した、わる数の分母と分子を入れかえて計算する方法と同じ答えになりました。なぜ、わる数を逆数にしなければいけないのか理由がわかっていただけたでしょうか。
