算数の台形の面積を公式を使って計算する方法

学習する学年：小学生

１．台形の形の説明

小学校の高学年になると、円、三角形、長方形などの図形の授業が始まります。

台形も図形の授業で学習する1つに含まれていますので、台形とはどんな形でどんな公式を使って面積を求めるのかをしっかり覚えてください。

台形とは、1組の向かい合った辺が平行である四辺形（4つの辺で構成されている形）のことをいいます。

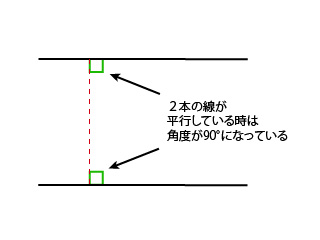
平行という言葉が出てきましたが、平行は何を表しているのかわかりますか？

平行は、どういうことを表しているのかというと、下の図のように、ある辺から垂直（90°の角度）に線を伸ばした時、その線ともう片方の辺も90°の角度になっている状態のことを平行といいます。

上の説明を読んで平行の意味がわかった方は、下に2つの図形がありますので、どちらが台形なのかを考えてみましょう？

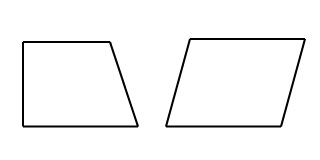
台形かどうかを判断するポイントは、

• 四辺形である
• 1組の向かい合った辺が平行である

という2つの特徴を持った図形を探すことです。

まずは、四辺形かどうかをみてみましょう。

それぞれの2つの図形は4つの辺で成り立っているので四辺形です。

この時点ではどちらの図形も台形の可能性があります。

次は、向かい合った辺が平行かどうかをみてみましょう。

左側の図形は1組の辺が平行になっていて、右側の図形は2組の辺が平行になっています。

台形とは1組の向かい合った辺が平行である四辺形のことでしたよね。

したがって、左側の図形が台形になります。

では、右側の図形は何の図形かというと平行四辺形です。

台形と平行四辺形は形がよく似ていますので、何組の辺が平行になっているのかを確かめて判断してください。

２．台形の面積を求める公式

小学生の時に、次のような台形の面積を求める公式を勉強しましたが覚えていますか。

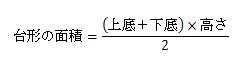
この公式はちゃんと理由があるんです。なぜそうなるのかをみていきましょう。

最初に、下の図を見てください。

台形を2つ用意します。1つの台形はそのままで、もう1つの台形は上下ひっくり返して台形を2つ連結してみます。

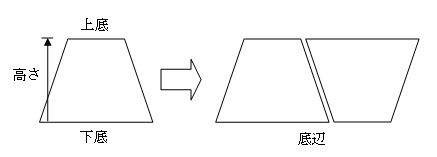
台形を2つ連結した図形はどこかで見覚えがありませんか？

あらびっくり。台形を2つくっつけたら平行四辺形になりました。

平行四辺形の面積を計算する式は、底辺×高さで求めることができますよね。

台形が2つの面積の式が底辺×高さということは、台形が1つの面積は（底辺×高さ）÷2になります。
※底辺とは、上底＋下底のことです。

したがって、学校で勉強した台形の面積を求める公式になりました。

では、下の台形の図形は2つ連結すると何の図形に変わるでしょうか？

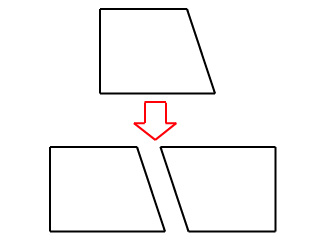
台形を2つくっつけると、長方形に変わりました。

長方形の面積を計算する式は、底辺×高さで求めることができますよね。

台形を2つ連結したら底辺×高さで面積が求められるということは、その面積を半分にすると台形の面積が求められそうです。

したがって、台形1個あたりの面積は、（底辺×高さ）÷2になります。
※底辺とは、上底＋下底のことです。

結局のところ、台形を2つくっつけて作った平行四辺形の面積も長方形の面積も、底辺×高さで求めることができるということです。

台形1つの面積を求める公式は、

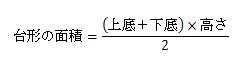
となり、学校で教わった式になります。

学校の先生に、かっこ、じょうていたすかてい、かっことじる、かけるたかさ、わるに、を呪文のように何回でも口に出して覚えるように言われましたよね。正しくその通りなので覚えてください。

３．台形の面積の計算方法

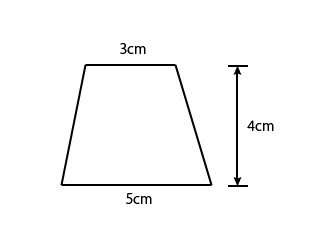
台形の面積を求める公式がわかってもらえたところで、次は実際に上の台形の面積を数値を使って計算してみましょう。

図形で与えられている数値を式に代入するだけで答えはでますので難しく考えなくても大丈夫です。

台形の面積の公式は次の式ですよね。

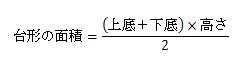
上の式を計算するのに必要な数値は、上底、下底、高さの数値なので、上の図形から値を読み取ってください。

読み取った値は次のようになります。

• 上底：3cm
• 下底：5cm
• 高さ：4cm

各数値が読み取れましたら、数値を式に代入して計算しましょう。

• 台形の面積＝（3cm＋5cm）×4cm/2

式を計算すると答えは16cm²になります。

なお、面積の単位は、cm²、m²のように2がつきますので間違えないようにしてください。